关于碰撞理论(Collision Theory)那点事儿

这里只总结关于使用碰撞理论进行表面碰撞（吸附）速率的推导。
先上个图吧，理解这里全靠这张图。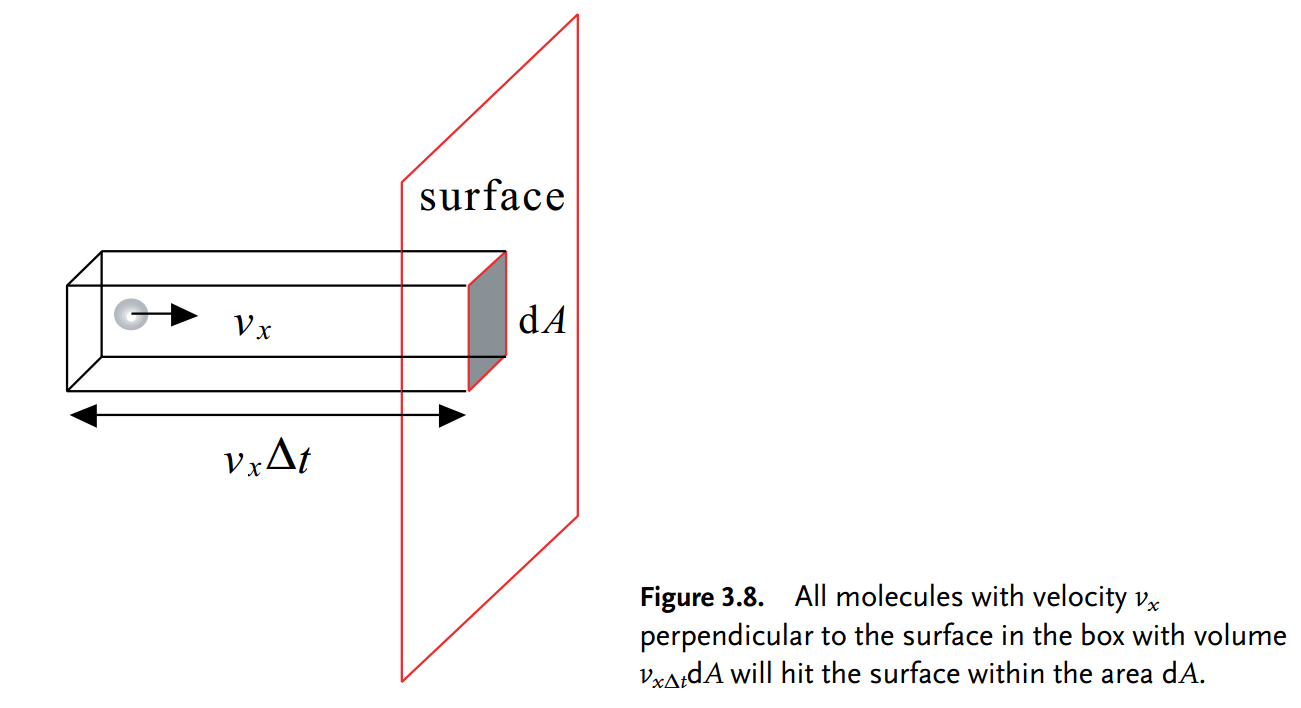


碰撞速率就是单位时间内单位面积分子碰撞到表面的次数。如图给定一个表面其面积为$A$, 若分子能够碰撞到表面则一定有垂直于表面的速率$v_{x}$。
所有分子的速率分布服从Boltzmann分布$f(v_{x})$。
若垂直于表面的速率为$v_{x}$的分子能在在给定时间$\Delta t$内能够撞到表面的话，则该分子距离表面的距离一定小于$v_{x}\Delta t$。
换一个角度理解就是，若在垂直于表面且体积为$V = v_{x}\Delta t A$的立方体之内的分子才能够撞到表面。
那就好办了，也就是说把这个体积求出来乘上分子的密度就得到时间$\Delta t$内撞到表面积为$A$的表面的分子数了。那速率也就可以得到了。于是有，
$$
r_{coll-surf} = \frac{1}{\Delta t A }\int_{0}^{\infty} f(v_{x})V(v_{x}) \rho dv_{x}
$$
其中$\int_{0}^{\infty} f(v_{x})V(v_{x}) \rho dv_{x}$就是能够碰撞到表面的分子总数
能够撞到表面的“体积” $V=v_{x}\Delta t A$也是速率的函数因此要放在里面一起积分。


于是碰撞速率就可推导出：
$$
r_{coll-surf} = \frac{1}{\Delta t A }\int_{0}^{\infty} f(v_{x})V(v_{x}) \rho dv_{x} = \rho \int_{0}^{\infty} v_{x} f(v_{x}) dv_{x} \\
= \frac{p}{k_{B}T} \int_{0}^{\infty} v_{x} \sqrt{\frac{m}{2\pi k_{B} T} } e^{- \frac{mv_{x}^{2}}{2k_{B}T}} dv_{x} \\
= \frac{p}{k_{B}T} \bar{v_{x}} = \frac{p}{k_{B}T} \sqrt{\frac{k_{B}T}{2\pi m}}
= \frac{p}{\sqrt{2 \pi m k_{B} T}}
$$