动力学蒙特卡洛(kinetic Mont Carlo)基本原理小结

克服模拟的时间尺度的局限

由于许多动态的过程(dynamic evolution)，例如表面的生长或者材料的老化，时间的跨度都在s以上，超出了分子动力学模拟的范围，动力学蒙特卡洛模拟便是针对这种长时间尺度的动态模拟的。

Kinetic Monte Carlo attempts to overcome this limitation by exploiting the fact that the long-time dynamics of this kind of system typically consists of diffusive jumps from state to state. Rather than following the trajectory through every vibrational period, these state-to-state transitions are treated directly

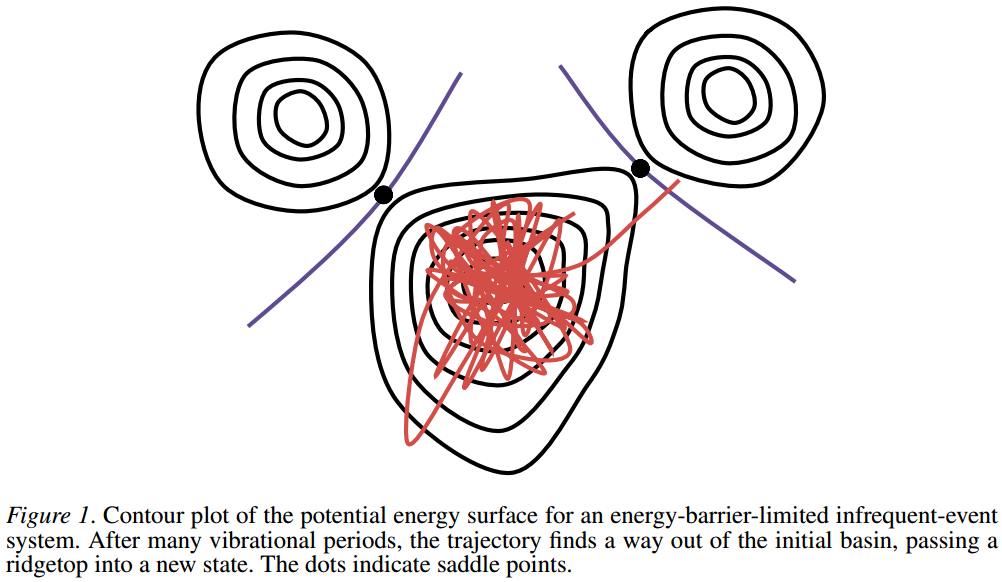
kMC从某种程度上就是对MD的一种粗化，将关注点从原子粗化到体系，将原子轨迹粗化到体系组态的跃迁，那么模拟的时间跨度就将从原子振动的尺度提高到组态跃迁的尺度，这是因为这种处理方法摈弃了与体系穿越势垒无关的微小振动，而只着眼于体系的组态变化。因此，虽然不能描绘原子的运动轨迹，但是作为体系演化，其“组态轨迹”仍然是正确的。
此外，因为组态变化的时间间隔很长，体系完成的连续两次演化是独立的，无记忆的，所以这个过程是一种典型的马尔可夫过程(Markov process)，及从组态 $i$ 跃迁到组态 $j$ ，这一过程只与跃迁速率 $k_{ij}$ 有关。

for each possible escape pathway to an adjacent basin, there is a rate constant $k_{ij}$ that characterizes the probability, per unit time, that it escapes to that state $j$

如果精确地知道 $k_{ij}$，我们便可以构造一个随机过程，使得体系按照正确的轨迹演化。这里正确的意思是某条给定演化轨迹出现的几率与MD模拟结果完全一致(假设我们进行了大量的MD模拟，每次模拟中每个原子的初始动量随机给定)。这种通过构造随机过程研究体系演化的方法即为动力学蒙特卡洛方法(kinetic Monte Carlo, KMC)

kMC的时间步长

这里算是kMC中比较重要的一点。
$k_{ij}$ 代表体系从组态 $i$ 逃逸到 $j$ 的速率，则发生跃迁的概率为 $k_{tot} = \sum_{j}^{}{k_{ij}}$
Gillespie给出的假设：

Suppose that the system is in configuration $c$. The probability that a particular enabled reaction $c \rightarrow c^{‘}$ occurs in an infinitesimal period $\delta t$ is given by $k_{c \rightarrow c^{‘}}*\delta t$.

则体系处在某一状态且经过$\delta t$之后体系状态未改变的概率为
$$P(T>= t + \delta t) = P(T>= t)(1 - k_{tot}\delta t)$$
将等式写成：
$$\frac{P(T>= t + \delta t) - P(T>= t)}{\delta t} = -k_{tot}P(T>= t)$$
积分后得到体系不发生跃迁的概率
$$P(T>= t) = exp(-k_{tot}t)$$
即，
$$p_{survive} = exp(-k_{tot}t)$$
则在时间t内体系发生跃迁的概率为
$$p_{transition} = 1 - p_{survive} = 1 - exp(-k_{tot}t)$$

可以看到逃逸概率呈指数分布，求其期望值便可得到逃逸所需的平均时间 $\tau$
$$\tau = \int_{0}^{\infty} tp(t)=\frac{1}{k_{tot}}$$

以上就是kMC中关于时间步长的推导了，也是kMC模拟程序中按照指数分布抽取随机数的原理。

步长的另一种推导方法

今天在kmos的那篇文章中有看到了使用Poission分布来推导体系时间推进公式的方法。
一般在不相关的两次事件的时间间隔是服从Possion分布的，也就意味着针对一个时间的发生速率$k$，则在时间间隔$\Delta t$内事件发生$n$次的概率为$p_{n}(k, \Delta t)$
$$p_{n}(k, \Delta t) = (k\Delta t)^{n}e^{-k\Delta t}/n!$$
则两次事件的间隔时间就为没有事件发生的间隔（也就是上文的$p_{survive}$）, 就是$n=0$时的$\Delta t$
$$p_{0}(k, \Delta t) = e^{-k\Delta t}$$
按照上文的方法可以得到kMC模拟中的时间步长
$$\Delta t = \frac{-ln(r)}{k}$$