Cluster Expansion中Projection Matrix的应用

这里只是记录下我对Cluster Expansion的理解，不一定正确。

首先对于直接使用DFT计算所有configuration表面上发生反应（如吸附，基元反应等）的能量是不现实的，耗资源耗时间。那么通过统一的公式对能量进行矫正可以将DFT算得能量进行延伸，得到不同configuration表面的相关能量的近似值，便是一种很方便的方法。

Cluster Expansion便是一种通过展开的方式将相互作用矫正项表达出来的一种方法。这种方法有点类似线性代数中的使用一组基向量展开，也就类似泰勒展开和傅立叶展开。

Cluster Expansion的方法

表面上每个位点的状态

在Cluster Expansion中首先要定义两个spin变量来表示表面位点的状态，因为表面的位点只有两个状态（被吸附物占据和未被占据），因此使用变量$\sigma = (+1/-1)$表示。

基

Cluster Expansion使用一组叫做$figure$的基将相互作用能矫正项进行多项式展开。这些基其实就是一系列的子图，由0到多个位点和线组成。如下图：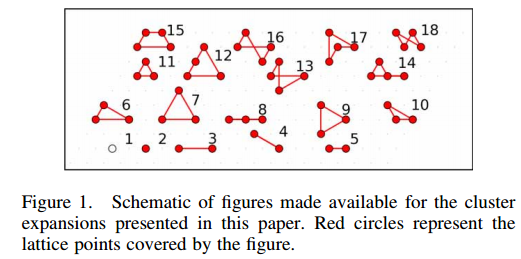

可见图中的这些基只展开到了四体相互作用，也就说明这个展开是有截断的，正常所有的子图可以组成一组无数维空间中的基，并且这些基相互正交（orthogonal）且完备（complete），但是由于有些距离比较远的相互作用对于整体的影响会很小，所以可以进行适当的截断。

展开三步走

需要将相互作用矫正项展开需要三步（打开冰箱门。。。

1. 针对某个位点某个$figure$进行spin变量的累积运算。
   $$\pi _{\alpha ,site} =\frac{1}{\nu _{\alpha}} \prod_{i=1}^{\nu _{\alpha}} \sigma _{i}$$
   其中，$\nu_{\alpha}$为这个$figure$中的site数。

2. 这对某个configuration中的所有点针对某个$figure$进行累加
   $$\Pi_{\alpha} = \frac{1}{N_{sites}}\sum_{j=1}^{N_{site}}{\pi_{\alpha, j}}$$
   其中，$N_{sites}$是给定的configuration中的site总数。

3. 针对给定的configuration中所有对称性等价的$figure$的有2得到的求和值再次进行累加。
   $$\bar{\Pi}_{F} = \frac{\nu_{\alpha}}{N_{F}}\sum_{k=1}^{N_{F}}{\Pi_{F_{k}}}$$
   那这个值就是在一个configuration中针对一个$figure$的矫正项展开项了。

如果给定一个configuration，则相互作用能矫正项$F(\sigma)$可以表示为：
$$F(\sigma) = \sum_{i=1}^{N_{F}}{J_{i}\bar{\Pi}_{F_{i}}} $$

如果有多个configuration，则就会有多个这样子的多项式，$F_{0}(\sigma)$, $F_{1}(\sigma)$, $F_{2}(\sigma)$, …

获取系数$J_{i}$

展开的目的是为了得到展开的系数，这样知道了系数就可以根据多项式求任何configuration的矫正项的值了。
但是如何获取展开的系数呢？这就需要同时对多个configuration进行上面的展开操作，这样我们就会得到一组方程组：
$$F_{0}(\sigma) = \sum_{i=1}^{N_{F}}{J_{i}\bar{\Pi}^{0}_{F_{i}}} $$
$$F_{1}(\sigma) = \sum_{i=1}^{N_{F}}{J_{i}\bar{\Pi}^{1}_{F_{i}}} $$
$$:$$

这样我们就可以使用最小二乘法进行优化，得到拟合后的系数$J_{i}$:
目标函数$$F(J_{0}, J_{1}, …) = \sum_{j=0}^{N_{F}}({F_{j}(\sigma) - \sum_{i=1}^{N_{F}}{J_{i}\bar{\Pi}^{j}_{F_{i}}}})^{2}$$

投影矩阵用于拟合

其实仔细观察就会发现，展开的多项式都是线性的，因为spin变量的值就只有（+1/-1）两种。因此可以将上面的过程中的每个$\bar{\Pi}_{F_{i,j}}$放入到一个矩阵中，然后一些列的方程可以写成一个$Ax=b$的形式。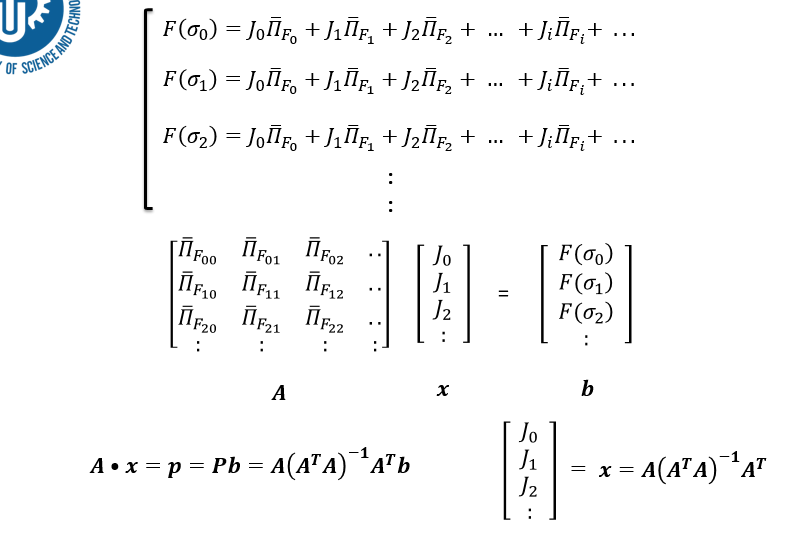

（图片截自组会的ppt）
这样整个过程就可以通过矩阵一次性处理了，要写程序的话也是方便的多，而且使用numpy或者matlab效率也会很高。