机器学习算法实践-朴素贝叶斯(Naive Bayes)

前言

上一篇总结了决策树的实现，本文中我将一步步实现一个朴素贝叶斯分类器，并采用SMS垃圾短信语料库中的数据进行模型训练，对垃圾短信进行过滤，在最后对分类的错误率进行了计算。

正文

与决策树分类和k近邻分类算法不同，贝叶斯分类主要借助概率论的知识来通过比较提供的数据属于每个类型的条件概率, 将他们分别计算出来然后预测具有最大条件概率的那个类别是最后的类别。当然样本越多我们统计的不同类型的特征值分布就越准确，使用此分布进行预测则会更加准确。

贝叶斯准则

朴素贝叶斯分类器中最核心的便是贝叶斯准则，他用如下的公式表示:
$$
p(c|x) = \frac{p(x|c)p(c)}{p(x)}
$$

此公式表示两个互换的条件概率之间的关系，他们通过联合概率关联起来，这样使得我们知道$p(B|A)$的情况下去计算$p(A|B)$成为了可能，而我们的贝叶斯模型便是通过贝叶斯准则去计算某个样本在不同类别条件下的条件概率并取具有最大条件概率的那个类型作为分类的预测结果。

使用条件概率来进行分类

这里我通俗的介绍下如何通过条件概率来进行分类，假设我们看到了一个人的背影，想通过他背影的一些特征(数据)来判断这个人的性别(类别)，假设其中涉及到的特征有: 是否是长发, 身高是否在170以上，腿细，是否穿裙子。当我们看到一个背影便会得到一个特征向量用来描述上述特征(1表示是，0表示否): $\omega = [0, 1, 1, 0]$

贝叶斯分类便是比较如下两个条件概率:

  1. $p(男生 | \omega)$，$\omega$ 等于 $[0, 1, 1, 0]$ 的条件下此人是男生的概率
  2. $p(女生 | \omega)$，$\omega$ 等于 $[0, 1, 1, 0]$ 的条件下此人是女生的概率

若$p(男生 | \omega) > p(女生 | \omega)$, 则判定此人为男生, 否则为女生

那么$p(男生 | \omega)$ 怎么求呢? 这就要上贝叶斯准则了

根据贝叶斯准则，
$$
p(男生 | \omega) = \frac{p(\omega | 男生)p(男生)}{p(\omega)}
$$
写成好理解些的便是:
$$
p(男生 | 短发且身高在170以上且腿细且不穿裙子) = \frac{p(短发且身高在170以上且腿细且不穿裙子 | 男生)p(男生)}{p(短发且身高在170以上且腿细且不穿裙子)}
$$

如果特征之间都是相互独立的(条件独立性假设)，那么便可以将上述条件概率改写成:

$$
p(短发且身高在170以上且腿细且不穿裙子 | 男生) = p(短发 | 男生) * p(170以上 | 男生) * p(腿细 | 男生) * p(没穿裙子 | 男生)
$$

这样我们就能计算当前这个背影属于男生和属于女生的条件概率了。

实现自己的贝叶斯分类器

贝叶斯分类器实现起来非常的简单, 下面我以进行文本分类为目的使用Python实现一个朴素贝叶斯文本分类器.

为了计算条件概率，我们需要计算各个特征的在不同类别下的条件概率以及类型的边际概率，这就需要我们通过大量的训练数据进行统计获取近似值了，这也就是我们训练我们朴素贝叶斯模型的过程.

针对不同的文本，我们可以将所有出现的单词作为数据特征向量，统计每个文本中出现词条的数目(或者是否出现某个词条)作为数据向量。这样一个文本就可以处理成一个整数列表，并且长度是所有词条的数目，这个向量也许会很长，用于本文的数据集中的短信词条大概一共3000多个单词。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def get_doc_vector(words, vocabulary):
    ''' 根据词汇表将文档中的词条转换成文档向量

    :param words: 文档中的词条列表
    :type words: list of str

    :param vocabulary: 总的词汇列表
    :type vocabulary: list of str

    :return doc_vect: 用于贝叶斯分析的文档向量
    :type doc_vect: list of int
    '''
    doc_vect = [0]*len(vocabulary)

    for word in words:
        if word in vocabulary:
            idx = vocabulary.index(word)
            doc_vect[idx] = 1

    return doc_vect

统计训练的过程的代码实现如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def train(self, dataset, classes):
    ''' 训练朴素贝叶斯模型

    :param dataset: 所有的文档数据向量
    :type dataset: MxN matrix containing all doc vectors.

    :param classes: 所有文档的类型
    :type classes: 1xN list

    :return cond_probs: 训练得到的条件概率矩阵
    :type cond_probs: dict

    :return cls_probs: 各种类型的概率
    :type cls_probs: dict
    '''
    # 按照不同类型记性分类
    sub_datasets = defaultdict(lambda: [])
    cls_cnt = defaultdict(lambda: 0)

    for doc_vect, cls in zip(dataset, classes):
        sub_datasets[cls].append(doc_vect)
        cls_cnt[cls] += 1

    # 计算类型概率
    cls_probs = {k: v/len(classes) for k, v in cls_cnt.items()}

    # 计算不同类型的条件概率
    cond_probs = {}
    dataset = np.array(dataset)
    for cls, sub_dataset in sub_datasets.items():
        sub_dataset = np.array(sub_dataset)
        # Improve the classifier.
        cond_prob_vect = np.log((np.sum(sub_dataset, axis=0) + 1)/(np.sum(dataset) + 2))
        cond_probs[cls] = cond_prob_vect

    return cond_probs, cls_probs

注意这里对于基本的条件概率直接相乘有两处改进:

  1. 各个特征的概率初始值为1，分母上统计的某一类型的样本总数的初始值是1，这是为了避免如果有一个特征统计的概率为0，则联合概率也为零那自然没有什么意义了, 如果训练样本足够大时，并不会对比较结果产生影响.
  2. 由于各个独立特征的概率都是小于1的数，累积起来必然会是个更小的书，这会遇到浮点数下溢的问题，因此在这里我们对所有的概率都取了对数处理，这样在保证不会有损失的情况下避免了下溢的问题。

获取了统计概率信息后，我们便可以通过贝叶斯准则预测我们数据的类型了，这里我并没有直接计算每种情况的概率，而是通过统计得到的向量与数据向量进行内积获取条件概率的相对值并进行相对比较做出决策的。

1
2
3
4
5
6
7
8
def classify(self, doc_vect, cond_probs, cls_probs):
    ''' 使用朴素贝叶斯将doc_vect进行分类.
    '''
    pred_probs = {}
    for cls, cls_prob in cls_probs.items():
        cond_prob_vect = cond_probs[cls]
        pred_probs[cls] = np.sum(cond_prob_vect*doc_vect) + np.log(cls_prob)
    return max(pred_probs, key=pred_probs.get)

进行短信分类

已经构建好了朴素贝叶斯模型，我们就可以使用此模型来统计数据并用来预测了。这里我使用了SMS垃圾短信语料库中的垃圾短信数据, 并随机抽取90%的数据作为训练数据，剩下10%的数据作为测试数据来测试我们的贝叶斯模型预测的准确性。

当然在建立模型前我们需要将数据处理成模型能够处理的格式:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
ENCODING = 'ISO-8859-1'
TRAIN_PERCENTAGE = 0.9

def get_doc_vector(words, vocabulary):
    ''' 根据词汇表将文档中的词条转换成文档向量

    :param words: 文档中的词条列表
    :type words: list of str

    :param vocabulary: 总的词汇列表
    :type vocabulary: list of str

    :return doc_vect: 用于贝叶斯分析的文档向量
    :type doc_vect: list of int
    '''
    doc_vect = [0]*len(vocabulary)

    for word in words:
        if word in vocabulary:
            idx = vocabulary.index(word)
            doc_vect[idx] = 1

    return doc_vect

def parse_line(line):
    ''' 解析数据集中的每一行返回词条向量和短信类型.
    '''
    cls = line.split(',')[-1].strip()
    content = ','.join(line.split(',')[: -1])
    word_vect = [word.lower() for word in re.split(r'\W+', content) if word]
    return word_vect, cls

def parse_file(filename):
    ''' 解析文件中的数据
    '''
    vocabulary, word_vects, classes = [], [], []
    with open(filename, 'r', encoding=ENCODING) as f:
        for line in f:
            if line:
                word_vect, cls = parse_line(line)
                vocabulary.extend(word_vect)
                word_vects.append(word_vect)
                classes.append(cls)
    vocabulary = list(set(vocabulary))

    return vocabulary, word_vects, classes

有了上面三个函数我们就可以直接将我们的文本转换成模型需要的数据向量，之后我们就可以划分数据集并将训练数据集给贝叶斯模型进行统计。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 训练数据 & 测试数据
ntest = int(len(classes)*(1-TRAIN_PERCENTAGE))

test_word_vects = []
test_classes = []
for i in range(ntest):
    idx = random.randint(0, len(word_vects)-1)
    test_word_vects.append(word_vects.pop(idx))
    test_classes.append(classes.pop(idx))

train_word_vects = word_vects
train_classes = classes

train_dataset = [get_doc_vector(words, vocabulary) for words in train_word_vects]

训练模型:
1
cond_probs, cls_probs = clf.train(train_dataset, train_classes)

剩下我们用测试数据来测试我们贝叶斯模型的预测准确度:

1
2
3
4
5
6
7
8
9
10
# 测试模型
error = 0
for test_word_vect, test_cls in zip(test_word_vects, test_classes):
    test_data = get_doc_vector(test_word_vect, vocabulary)
    pred_cls = clf.classify(test_data, cond_probs, cls_probs)
    if test_cls != pred_cls:
        print('Predict: {} -- Actual: {}'.format(pred_cls, test_cls))
        error += 1

print('Error Rate: {}'.format(error/len(test_classes)))

随机测了四组，错误率分别为:0, 0.037, 0.015, 0. 平均错误率为1.3%

测完了我们尝试下看看不同类型短信各个词条的概率分布是怎样的吧:

1
2
3
4
5
6
7
8
9
10
11
# 绘制不同类型的概率分布曲线
fig = plt.figure()
ax = fig.add_subplot(111)
for cls, probs in cond_probs.items():
    ax.scatter(np.arange(0, len(probs)),
               probs*cls_probs[cls],
               label=cls,
               alpha=0.3)
    ax.legend()

plt.show()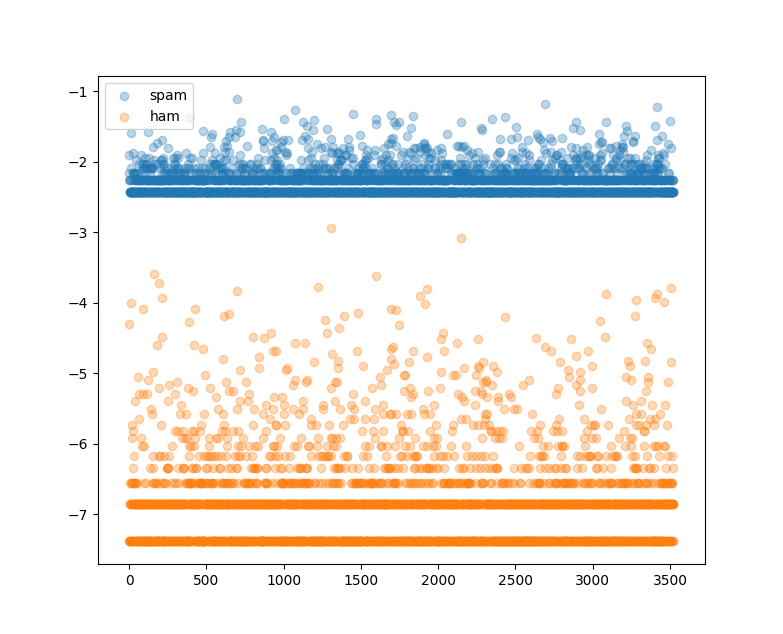

试试决策树

上一篇我们基于ID3算法实现了决策树，同样是分类问题，我们同样可以使用我们的文本数据来构建用于分类短信的决策树，当然唯一比较麻烦的地方在于如果按照与贝叶斯相同的向量作为数据，则属性可能会非常多，我们在构建决策树的时候每层树结构都是递归通过遍历属性根据信息增益来选取最佳属性进行树分裂的，这样很多的属性可能会对构建决策树这一过程来说会比较耗时.那我们就试试吧…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 生成决策树
if not os.path.exists('sms_tree.pkl'):
    clf.create_tree(train_dataset, train_classes, vocabulary)
    clf.dump_tree('sms_tree.pkl')
else:
    clf.load_tree('sms_tree.pkl')

# 测试模型
error = 0
for test_word_vect, test_cls in zip(test_word_vects, test_classes):
    test_data = get_doc_vector(test_word_vect, vocabulary)
    pred_cls = clf.classify(test_data, feat_names=vocabulary)
    if test_cls != pred_cls:
        print('Predict: {} -- Actual: {}'.format(pred_cls, test_cls))
        error += 1

print('Error Rate: {}'.format(error/len(test_classes)))

随机测了两次，错误率分别为:0.09, 0.0

效果还算不错

我们还是用Graphviz可视化看一下决策树都选取了那些词条作为判别标准(这时候决策树的好处就体现出来了)。


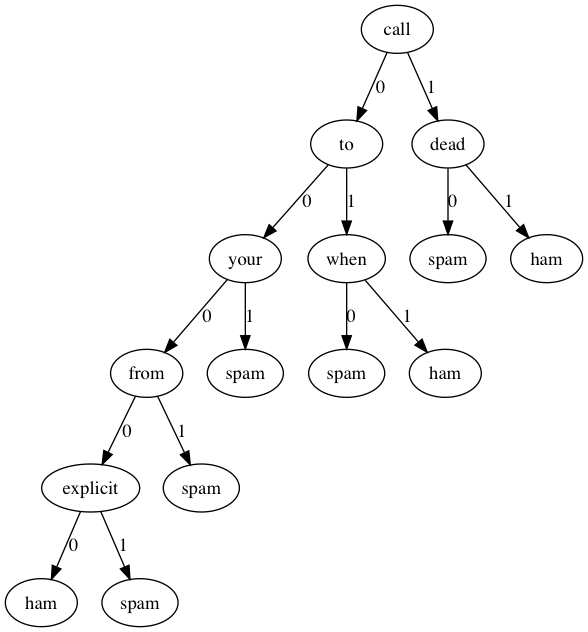
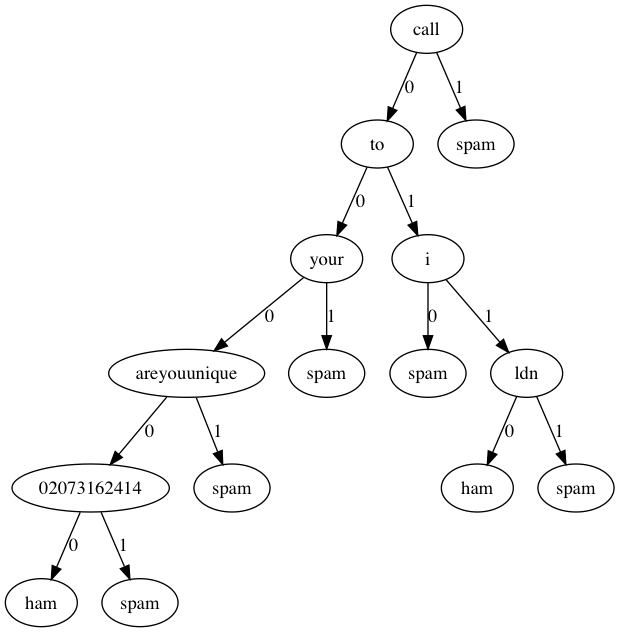
可见决策树的深度并不是很深，如果分类类型一多，估计深度增加上去决策树可能会有些麻烦。

总结

本文我们使用Python一步步实现了朴素贝叶斯分类器，并对短信进行了垃圾短信过滤，同样的数据我们同决策树的分类效果进行了简单的比较。本文相关代码实现:https://github.com/PytLab/MLBox/tree/master/naive_bayes 。决策树过滤垃圾短信的脚本在https://github.com/PytLab/MLBox/tree/master/decision_tree

参考

相关阅读

Comments

▲