机器学习算法实践-Logistic回归与梯度上升算法(下)

前言

上篇主要总结了Logistic回归模型建立的理论基础，主要包含模型似然函数的建立以及梯度上升算法的优化推导。本文在上文的基础上使用Python一步步实现一个Logistic回归分类器，并分别使用梯度上升和随机梯度上升算法实现，对二维数据点分类进行可视化，最后使用之前使用过的SMS垃圾短信语料库中的短信数据进行模型训练并对短信数据进行分类。

正文

加载数据

从文件中读取特征以及类别标签用于优化模型参数

def load_data(filename):
    dataset, labels = [], []
    with open(filename, 'r') as f:
        for line in f:
            splited_line = [float(i) for i in line.strip().split('\t')]
            data, label = [1.0] + splited_line[: -1], splited_line[-1]
            dataset.append(data)
            labels.append(label)
    dataset = np.array(dataset)
    labels = np.array(labels)

    return dataset, labels

使用梯度上升算法

上文对Logistic回归模型使用梯度上升算法优化参数进行了理论介绍，这里就最先使用梯度上升算法来构建一个分类器.

首先我们是Sigmoid函数:

def sigmoid(x):
    ''' Sigmoid 阶跃函数
    '''
    return 1.0/(1 + np.exp(-x))

然后是梯度上升算法的实现:

def gradient_ascent(self, dataset, labels, max_iter=10000):
    ''' 使用梯度上升优化Logistic回归模型参数

    :param dataset: 数据特征矩阵
    :type dataset: MxN numpy matrix

    :param labels: 数据集对应的类型向量
    :type labels: Nx1 numpy matrix
    '''
    dataset = np.matrix(dataset)
    vlabels = np.matrix(labels).reshape(-1, 1)
    m, n = dataset.shape
    w = np.ones((n, 1))
    alpha = 0.001
    ws = []
    for i in range(max_iter):
        error = vlabels - self.sigmoid(dataset*w)
        w += alpha*dataset.T*error
        ws.append(w.reshape(1, -1).tolist()[0])

    self.w = w

    return w, np.array(ws)

在这里的数据操作都转换成Numpy矩阵的操作，主要是方便处理避免Python循环处理。同时每次梯度上升迭代过程中都把自变量，也就是Logistic模型参数进行收集，方便最后查看参数收敛情况。

关于梯度上升算法中，我们每次沿着梯度方向移动的步长 $\alpha$ 都设的固定距离为0.001，并没有做一维搜索。

可视化决策边界

Sigmoid函数的特点就是通过0点来进行分类，$\overline{x}^{T} \centerdot \overline{\omega}$ 的值小于0为一类，大于0位另外一类，因此我们可以通过 $\overline{x}^{T} \centerdot \overline{\omega} = 0$ 来获取分界线或者超平面。在二维平面里，我们可以通过求解 $w_{0}x_{0} + w_{1}x_{0}$(其中 $x_{0} = 1$) 并绘制直线来可视化决策边界。

def snapshot(w, dataset, labels, pic_name):
    ''' 绘制类型分割线图
    '''
    if not os.path.exists('./snapshots'):
        os.mkdir('./snapshots')

    fig = plt.figure()
    ax = fig.add_subplot(111)

    pts = {}
    for data, label in zip(dataset.tolist(), labels.tolist()):
        pts.setdefault(label, [data]).append(data)

    for label, data in pts.items():
        data = np.array(data)
        plt.scatter(data[:, 1], data[:, 2], label=label, alpha=0.5)

    # 分割线绘制
    def get_y(x, w):
        w0, w1, w2 = w
        return (-w0 - w1*x)/w2

    x = [-4.0, 3.0]
    y = [get_y(i, w) for i in x]

    plt.plot(x, y, linewidth=2, color='#FB4A42')

    pic_name = './snapshots/{}'.format(pic_name)
    fig.savefig(pic_name)
    plt.close(fig)

好了，优化算法和可视化代码都具备了，我们便可以拟合我们的数据了，这里使用两种类型的二维数据点来训练模型, 数据见https://github.com/PytLab/MLBox/blob/master/logistic_regression/testSet.txt

if '__main__' == __name__:
    clf = LogisticRegressionClassifier()
    dataset, labels = load_data('testSet.txt')
    w, ws = clf.gradient_ascent(dataset, labels, max_iter=50000)
    m, n = ws.shape

    # 绘制分割线
    for i in range(300):
        if i % (30) == 0:
            print('{}.png saved'.format(i))
            snapshot(ws[i].tolist(), dataset, labels, '{}.png'.format(i))

    fig = plt.figure()
    for i in range(n):
        label = 'w{}'.format(i)
        ax = fig.add_subplot(n, 1, i+1)
        ax.plot(ws[:, i], label=label)
        ax.legend()

    fig.savefig('w_traj.png')

通过将迭代过程中的权重参数输出，我们可以绘制决策边界的变化，看到参数的优化过程:

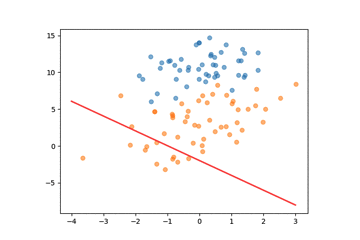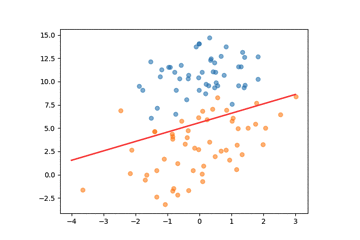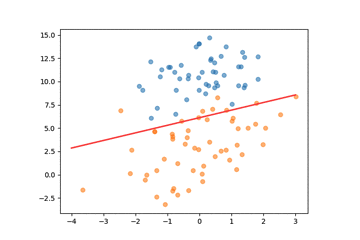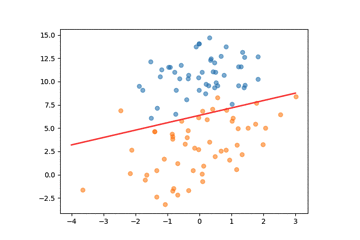
下面我们可视化一下模型参数在梯度上升过程中的收敛情况，我们总共迭代了50000步：

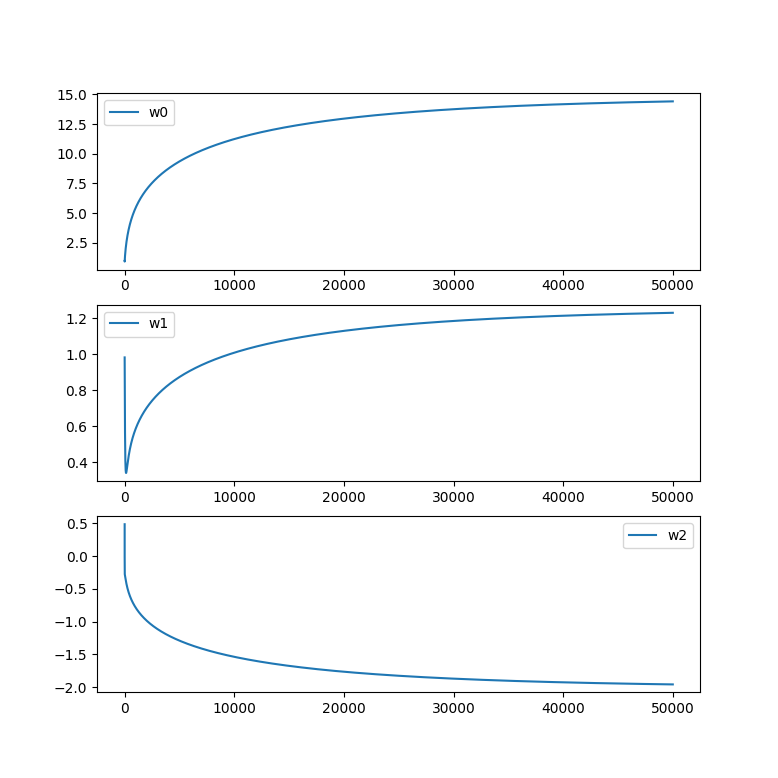
使用随机随机梯度上升算法

从求目标函数梯度的公式
$$
\nabla ln\mathcal{L}(\overline{\omega}) = \overline{x} \centerdot (\overline{y} - \overline{\pi(\overline{x})}) = \overline{x} \centerdot \overline{error}
$$
和实现代码

1 2	error = vlabels - self.sigmoid(datasetw) w += alphadataset.T*error

中我们可以看到，在使用梯度上升算法优化的时候每次迭代都需要使用所有的训练数据乘上误差向量，如果样本只有几百个那还好，如果有数十亿样本，那这个矩阵乘法将会非常的大，于是我们可以考虑使用随机梯度上升来更新 $\omega$, 所谓随机梯度就是指更新 $\omega$ 的时候不需要用所有的数据矩阵和误差矩阵乘积来更新，而是使用样本中随机选出的一个数据点来计算梯度并更新。这样可以在新的样本到来时对分类器进行增量式更新，因而随机梯度算法是一个在线学习算法, 之前的梯度上升算法是一次性处理所有样本数据被称作是批处理。

下面我们就重新写一个通过随机梯度上升算法优化的Logistic回归分类器

from logreg_grad_ascent import LogisticRegressionClassifier as BaseClassifer
from logreg_grad_ascent import load_data, snapshot

class LogisticRegressionClassifier(BaseClassifer):

    def stoch_gradient_ascent(self, dataset, labels, max_iter=150):
        ''' 使用随机梯度上升算法优化Logistic回归模型参数
        '''
        dataset = np.matrix(dataset)
        m, n = dataset.shape
        w = np.matrix(np.ones((n, 1)))
        ws = []

        for i in range(max_iter):
            data_indices = list(range(m))
            random.shuffle(data_indices)
            for j, idx in enumerate(data_indices):
                data, label = dataset[idx], labels[idx]
                error = label - self.sigmoid((data*w).tolist()[0][0])
                alpha = 4/(1 + j + i) + 0.01
                w += alpha*data.T*error
                ws.append(w.T.tolist()[0])

        self.w = w

        return w, np.array(ws)

我们写一个继承与刚才实现的分类器的派生类，并实现随机梯度算法，这里沿着梯度方向的步长随着迭代会逐渐减小来减弱参数的博定。

我们同样来可视化决策边界和参数的收敛曲线来看看随机梯度下降法对模型的优化过程:

if '__main__' == __name__:
    clf = LogisticRegressionClassifier()
    dataset, labels = load_data('testSet.txt')
    w, ws = clf.stoch_gradient_ascent(dataset, labels, max_iter=500)
    m, n = ws.shape

    # 绘制分割线
    for i, w in enumerate(ws):
        if i % (m//10) == 0:
            print('{}.png saved'.format(i))
            snapshot(w.tolist(), dataset, labels, '{}.png'.format(i))

    fig = plt.figure()
    for i in range(n):
        label = 'w{}'.format(i)
        ax = fig.add_subplot(n, 1, i+1)
        ax.plot(ws[:, i], label=label)
        ax.legend()

    fig.savefig('stoch_grad_ascent_params.png')

决策线变化: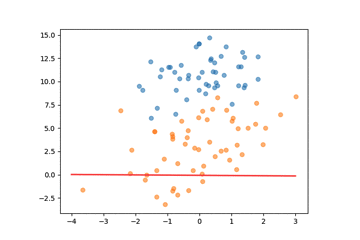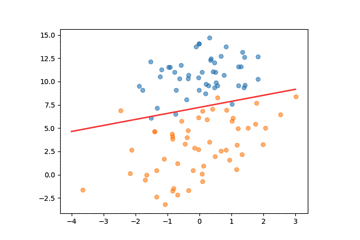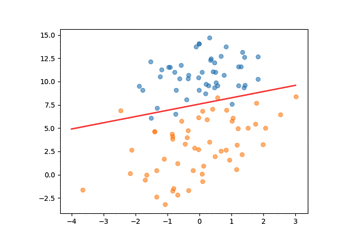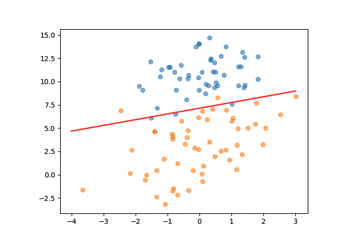

参数收敛曲线: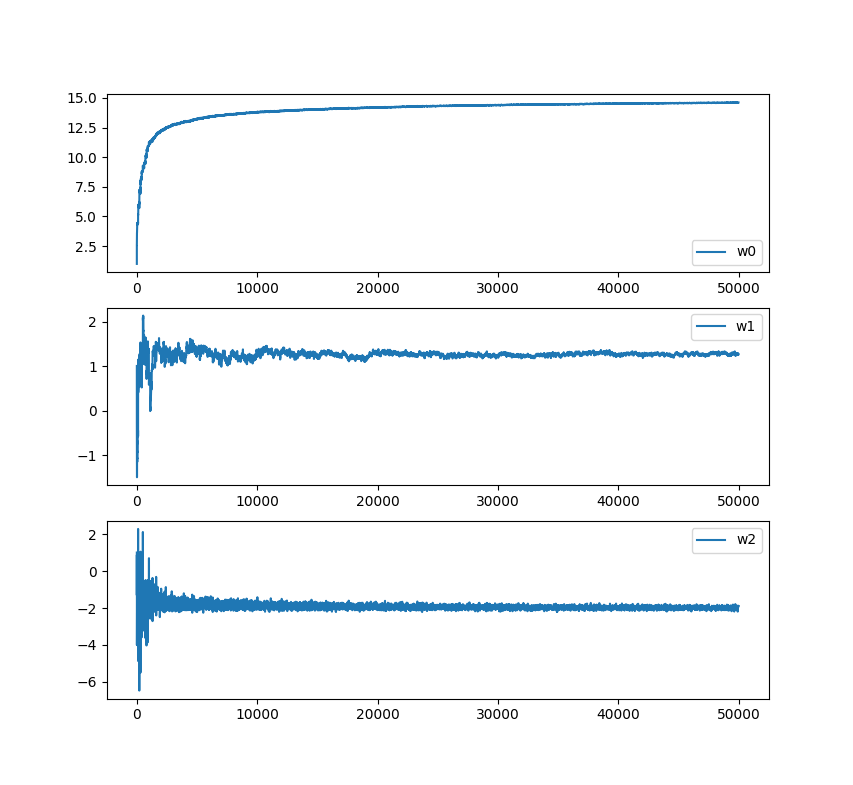

使用Logistic回归分类器分类短信

这里我还是使用了前两篇决策树和贝叶斯分类器使用的垃圾短信数据集来训练Logistic回归分类器，这时候对于Logistic分类器的参数可能会比较多，我们使用随机梯度上升算法来优化参数，相对于贝叶斯分类器，基于随机梯度上升算法的Logistic回归分类器对于维数较高的的数据向量和数量较大的数据集的训练速度还是有待改善的，我们同样使用留存交叉验证的方式来训练和测试模型，测试了三次Logistic回归模型对于垃圾短信的识别错误率分别为: 0.0833, 0.038, 0.038.

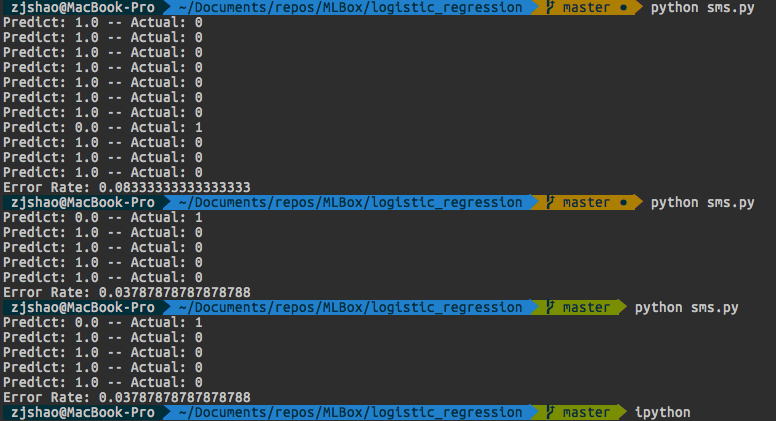
平均错误率为5.3%。可见我们的Logistic回归分类器也能较好的对垃圾短信文本进行识别。

总结

本文总结了Logistic回归和相关的优化算法(梯度上升以及随机梯度上升)的理论和代码实现，并对实现的模型进行了训练和测试。