机器学习算法实践-Platt SMO和遗传算法优化SVM

前言

之前实现了简单的SMO算法来优化SVM的对偶问题，其中在选取$\alpha$的时候使用的是两重循环通过完全随机的方式选取，具体的实现参考《机器学习算法实践-SVM中的SMO算法》。

本文在之前简化版SMO算法的基础上实现了使用启发式选取$\alpha$对的方式的Platt SMO算法来优化SVM。另外由于最近自己也实现了一个遗传算法框架GAFT，便也尝试使用遗传算法对于SVM的原始形式进行了优化。

对于本文算法的相应实现，参考:https://github.com/PytLab/MLBox/tree/master/svm
遗传算法框架GAFT项目地址: https://github.com/PytLab/gaft

正文

SMO中启发式选择变量

在SMO算法中，我们每次需要选取一对$\alpha$来进行优化，通过启发式的选取我们可以更高效的选取待优化的变量使得目标函数下降的最快。

针对第一个$\alpha_1$和第二个$\alpha_2$ Platt SMO采取不同的启发式手段。

第一个变量的选择

第一个变量的选择为外循环，与之前便利整个$\alpha$列表不同，在这里我们在整个样本集和非边界样本集间进行交替:

首先我们对整个训练集进行遍历, 检查是否违反KKT条件，如果改点的$\alpha_i$和$x_i, y_i$违反了KKT条件则说明改点需要进行优化。
Karush-Kuhn-Tucker(KKT)条件是正定二次规划问题最优点的充分必要条件。针对SVM对偶问题，KKT条件非常简单:
$$
\begin{cases}
\alpha_i = 0 \Longleftrightarrow y_i(w^{T}x_i + b) \ge 1 \\
\alpha_i = C \Longleftrightarrow y_i(w^{T}x_i + b) \le 1 \\
0 < \alpha_i < C \Longleftrightarrow y_i(w^{T}x_i + b) = 1
\end{cases}
$$
在遍历了整个训练集并优化了相应的$\alpha$后第二轮迭代我们仅仅需要遍历其中的非边界$\alpha$. 所谓的非边界$\alpha$就是指那些不等于边界0或者C的$\alpha$值。同样这些点仍然需要检查是否违反KKT条件并进行优化.

之后就是不断地在两个数据集中来回交替，最终所有的$\alpha$都满足KKT条件的时候，算法中止。

为了能够快速选取有最大步长的$\alpha$，我们需要对所有数据对应的误差进行缓存，因此特地写了个SVMUtil类来保存svm中重要的变量以及一些辅助方法:

class SVMUtil(object):
    '''
    Struct to save all important values in SVM.
    '''
    def __init__(self, dataset, labels, C, tolerance=0.001):
        self.dataset, self.labels, self.C = dataset, labels, C

        self.m, self.n = np.array(dataset).shape
        self.alphas = np.zeros(self.m)
        self.b = 0
        self.tolerance = tolerance
        # Cached errors ,f(x_i) - y_i
        self.errors = [self.get_error(i) for i in range(self.m)]

    # 其他方法...
...

下面为第一个变量选择交替遍历的大致代码，相应完整的Python实现(完整实现见https://github.com/PytLab/MLBox/blob/master/svm/svm_platt_smo.py):

while (it < max_iter):
    pair_changed = 0
    if entire:
        for i in range(svm_util.m):
            pair_changed += examine_example(i, svm_util)
            print('Full set - iter: {}, pair changed: {}'.format(i, pair_changed))
    else:
        alphas = svm_util.alphas
        non_bound_indices = [i for i in range(svm_util.m)
                             if alphas[i] > 0 and alphas[i] < C]
        for i in non_bound_indices:
            pair_changed += examine_example(i, svm_util)

    ...
...

第二个变量的选择

SMO中的第二个变量的选择过程为内循环，当我们已经选取第一个$\alpha_1$之后，我们希望我们选取的第二个变量$\alpha_2$优化后能有较大的变化。根据我们之前推导的式子$\alpha_{2}^{new, unclipped} = \alpha_{2}^{old} + \frac{y_{2}(E_{1} - E_{2})}{\eta}$ 可以知道，新的$\alpha_2$的变化依赖于$\lvert E_1 - E_2 \rvert$, 当$E_1$为正时，那么选择最小的$E_i$作为$E_2$，通常将每个样本的$E_i$缓存到一个列表中，通过在列表中选择具有$\lvert E_1 - E_2 \rvert$的$\alpha_2$来近似最大化步长。

有时候按照上述的启发式方式仍不能够是的函数值有足够的下降，这是按下述步骤进行选择:

在非边界数据集上选择能够使函数值足够下降的样本作为第二个变量
如果非边界数据集上没有，则在整个数据仅上进行第二个变量的选择
如果仍然没有则重新选择第一个$\alpha_1$

第二个变量选取的Python实现:

def select_j(i, svm_util):
    ''' 通过最大化步长的方式来获取第二个alpha值的索引.
    '''
    errors = svm_util.errors
    valid_indices = [i for i, a in enumerate(svm_util.alphas) if 0 < a < svm_util.C]

    if len(valid_indices) > 1:
        j = -1
        max_delta = 0
        for k in valid_indices:
            if k == i:
                continue
            delta = abs(errors[i] - errors[j])
            if delta > max_delta:
                j = k
                max_delta = delta
    else:
        j = select_j_rand(i, svm_util.m)
    return j

KKT条件允许一定的误差

在Platt论文中的KKT条件的判断中有一个tolerance允许一定的误差，相应的Python实现：

r = E_i*y_i

# 是否违反KKT条件
if (r < -tolerance and alpha < C) or (r > tolerance and alpha > 0):
    ...

关于Platt SMO的完整实现详见:https://github.com/PytLab/MLBox/blob/master/svm/svm_platt_smo.py

针对之前的数据集我们使用Platt SMO进行优化可以得到：

1 2	w = [0.8289668843516077, -0.26578914269411114] b = -3.9292583040559448

将分割线和支持向量可视化：

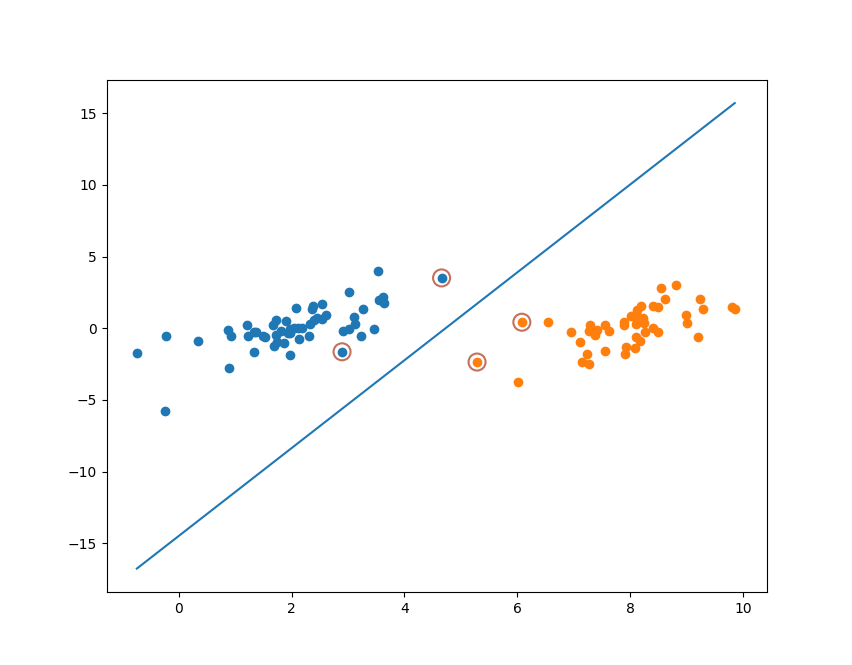
可见通过Platt SMO优化出来的支持向量与简化版的SMO算法有些许不同。

使用遗传算法优化SVM

由于最近自己写了个遗传算法框架，遗传算法作为一个启发式无导型的搜索算法非常易用，于是我就尝试使用遗传算法来优化SVM。

使用遗传算法优化，我们就可以直接优化SVM的最初形式了也就是最直观的形式:
$$
arg \max \limits_{w, b} \{ \min \limits_{n} (y_{i} \cdot (w^{T}x + b)) \cdot \frac{1}{\lVert w \rVert} \}
$$

顺便再安利下自己的遗传算法框架，在此框架的帮助下，优化SVM算法我们只需要写几十行的Python代码即可。其中最主要的就是编写适应度函数，根据上面的公式我们需要计算数据集中每个点到分割线的距离并返回最小的距离即可，然后放到遗传算法中进行进化迭代。

遗传算法框架GAFT项目地址: https://github.com/PytLab/gaft , 使用方法详见README。

Ok，我们开始构建种群用于进化迭代。

创建个体与种群

对于二维数据点，我们需要优化的参数只有三个也就是$[w_1, w_2]$和$b$, 个体的定义如下:

1
2
3

indv_template = GAIndividual(ranges=[(-2, 2), (-2, 2), (-5, 5)],
                             encoding='binary',
                             eps=[0.001, 0.001, 0.005])

种群大小这里取600，创建种群

1	population = GAPopulation(indv_template=indv_template, size=600).init()

创建遗传算子和GA引擎

这里没有什么特别的，直接使用框架中内置的算子就好了。

selection = RouletteWheelSelection()
crossover = UniformCrossover(pc=0.8, pe=0.5)
mutation = FlipBitBigMutation(pm=0.1, pbm=0.55, alpha=0.6)

engine = GAEngine(population=population, selection=selection,
                  crossover=crossover, mutation=mutation,
                  analysis=[ConsoleOutput, FitnessStore])

适应度函数

这一部分只要把上面svm初始形式描述出来就好了，只需要三行代码:

@engine.fitness_register
def fitness(indv):
    w, b = indv.variants[: -1], indv.variants[-1]
    min_dis = min([y*(np.dot(w, x) + b) for x, y in zip(dataset, labels)])
    return float(min_dis)

开始迭代

这里迭代300代种群

1 2	if '__main__' == __name__: engine.run(300)

绘制遗传算法优化的分割线

variants = engine.population.best_indv(engine.fitness).variants
w = variants[: -1]
b = variants[-1]

# 分类数据点
classified_pts = {'+1': [], '-1': []}
for point, label in zip(dataset, labels):
    if label == 1.0:
        classified_pts['+1'].append(point)
    else:
        classified_pts['-1'].append(point)

fig = plt.figure()
ax = fig.add_subplot(111)

# 绘制数据点
for label, pts in classified_pts.items():
    pts = np.array(pts)
    ax.scatter(pts[:, 0], pts[:, 1], label=label)

# 绘制分割线
x1, _ = max(dataset, key=lambda x: x[0])
x2, _ = min(dataset, key=lambda x: x[0])
a1, a2 = w
y1, y2 = (-b - a1*x1)/a2, (-b - a1*x2)/a2
ax.plot([x1, x2], [y1, y2])

plt.show()

得到的分割曲线如下图：

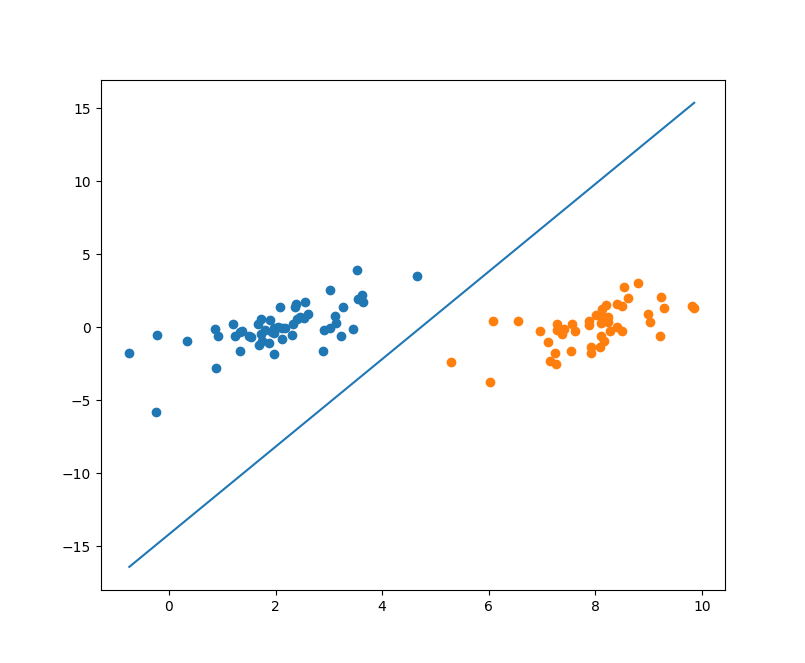
完整的代码详见: https://github.com/PytLab/MLBox/blob/master/svm/svm_ga.py

总结

本文对SVM的优化进行了介绍，主要实现了Platt SMO算法优化SVM模型，并尝试使用遗传算法框架GAFT对初始SVM进行了优化。

参考

Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines